01 Image Classification
Lecture 2: Summary
- The data-driven approach
- K-nearest neighbor
- Linear Classifiers
- Algebraic / Visual / Geometric viewpoints
- Softmax loss
Image Classification Task
이미지 분류는 컴퓨터 비전에서의 핵심 테스크이다.
이는 근본적 문제와 여러 어려움에 직면한다.
근본적으로, 인간과 컴퓨터의 정보 인지에는 차이가 존재한다.

그리고 몇가지 어려움으로는 광원의 변화, 변형, 가려짐, 혼잡한 배경, 클래스 내부 변동성 등이 있다.





How to classify?
이러한 어려움 속에서 어떻게 이미지를 분류할 수 있을까?
def classify_image(image):
# ...?
return class_label
이러한 모든 종류의 어려움을 단지, if-else 구문을 통해 분류할 수는 없다.
논리가 통하지 않는다면, 어떻게 분류를 할 수 있을까?
이를 위해 데이터를 이용한 접근을 수행하게 된다.
다수의 데이터를 이용하는 머신러닝 알고리즘으로 접근해보자.

머신러닝은 데이터를 이용하는 학습train과 학습을 바탕으로 정답을 맞추는 예측predict으로 스텝이 나눠진다.
Nearest Neighbor Classifier
알고리즘 수업에서 k-NN에 대해 배웠었다. k-NN은 어떤 데이터의 속성을 k개의 가까운 이웃의 속성을 보고 다수에 속하는 속성으로 분류하는 머신러닝 알고리즘이다.
k-NN에서 train은 단지 모든 훈련 데이터를 저장하는 일 뿐이다. 즉, 하는게 없다.
대신 predict 단계에서 많은 일을 한다. 모든 훈련 데이터 세트와 test_image와의 distance를 계산하고, 이 거리를 바탕으로 k-NN 정책에 따라 라벨을 분류한다.
L1 Distance(맨해튼 거리)를 사용한다고 가정할때, 이미지간의 거리 계산 방법은 다음과 같다.
각 칸은 픽셀값이다.
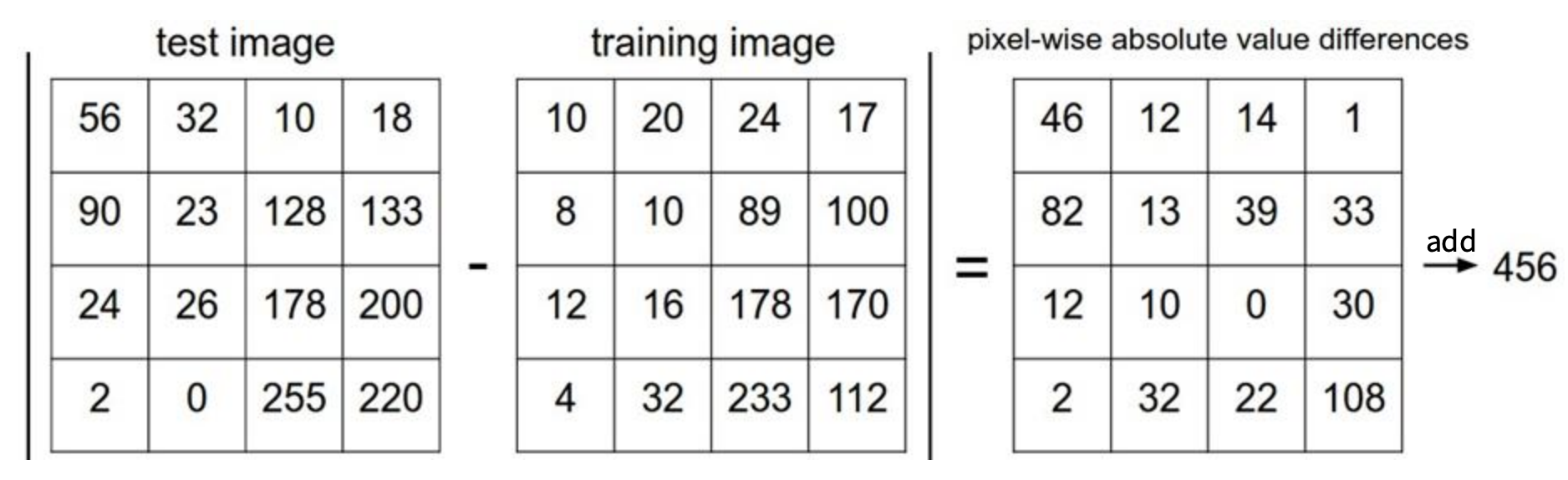
그런데 어떤 거리 척도를 택하냐에 따라 결과와 성능이 달라질 수 있다. 무엇을 선택해야 할까?
알고리즘 수업에서 공부한 것을 잠깐 꺼내와보자.
!Machine Learning Algorithm.#k-NN에 대한 기하학적 접근#거리 척도Distance Metric
따라서 특징 벡터의 각 요소들이 개별적 의미를 담고 있다면 L1 distance가 더 적합할 것이다. 반면, 각 요소의 실질적 의미가 모호한 경우에는 L2 distance가 더 적합할 수 있다.
k-NN on images never used
이러한 k-NN이 실제로 이미지에 대해 사용되지는 않는다.
(1) 일단 예측 비용이 너무 크고, (2) 예측 정확도도 크게 떨어지기 때문이다.
이미지에서 유사성을 판별하기 위한 특성 벡터는 픽셀이다. 32x32 픽셀인 두 그림간 유사성은 각 픽셀 위치와 RGB채널 값을 차원으로 하는 내적을 통해 이뤄질 수 있다. 이 경우 차원의 크기는 32x32x3 = 3072 이다.
e.g. R(1,1), G(1,1), B(1,1), ... , B(32,32).
이미지가 커질 수록 차원의 크기도 기하급수적으로 커지며, 이는 성능에 큰 문제를 끼친다.

k-NN은 학습 단계가 없고 예측 단계에서 모든 훈련 데이터와의 유사성(거리)을 계산한다. 매 이미지마다 분류를 위해 모든 훈련 세트에 대해 거리를 계산하는 것은 32픽셀 이미지라 할때, 32x32x3x(레이블의 훈련 이미지 수)x(레이블 수) 만큼의 계산을 해야 하는 것이다. 우리는 차라리 학습에서 더 많은 시간을 쓰길 원할 것이다.
또한 정확도마저 나쁘다. 픽셀들의 위치에 따른 distance metric이 공간적 위치 정보를 반영하지 못한다. 각각의 특성 벡터가 완전히 독립적으로 간주되어 나열되기 때문에 실제 공간상 거리와 방향은 물론 약간의 변형에도 취약해진다.

좀 더 자세한 내용은 Class Materials 1를 참조한다.
이러한 이유로 선형 분류기를 학습하며, 이 과정에서 공간적 정보를 반영하고자 한다.
Linear Classification
선형 분류기는 Neural Network의 핵심이다. NN는 선형 분류기를 벽돌처럼 쌓아 만드는 것이기 때문이다.
CIFAR10 데이터 세트를 바탕으로 분류기를 학습 시켜보자. 이 이미지들은 비행기, 오토바이, 새, 고양이 등 10개의 클래스로 구성되어 있다.

선형 분류기의 구조는 간단하게 아래 그림처럼 나타낼 수 있다.
이미지가 들어오면, 이 이미지를 분류기 f가 파라미터를 통해 계산하고 결과를 내놓는다.

f는 단지 이미지 x와 파라미터 W간의 매트릭스 연산을 의미한다.
그렇다면 그 결과 10개의 차원을 가진 벡터가 각 차원에 10개의 분류에 해당하는 점수를 산출하게 된다.
여기에 바이어스 b는 결과 차원과 동일한 값을 더해주게 된다. 바이어스가 필요한 이유는 잠시 뒤 기하적 관점에서 설명된다.

이때 차원을 맞춰주는 것이 매우 중요하다. 이를 이해하기 위해서는 선형대수학의 기초가 필요하다.
간단한 상황으로 예시를 들어보자
다음은 x = 1x4 인 4픽셀 1채널 이미지이다. 분류 클래스는 3이다.
따라서 학습이 끝난 파라미터 W는 3x4 매트릭스 이다.
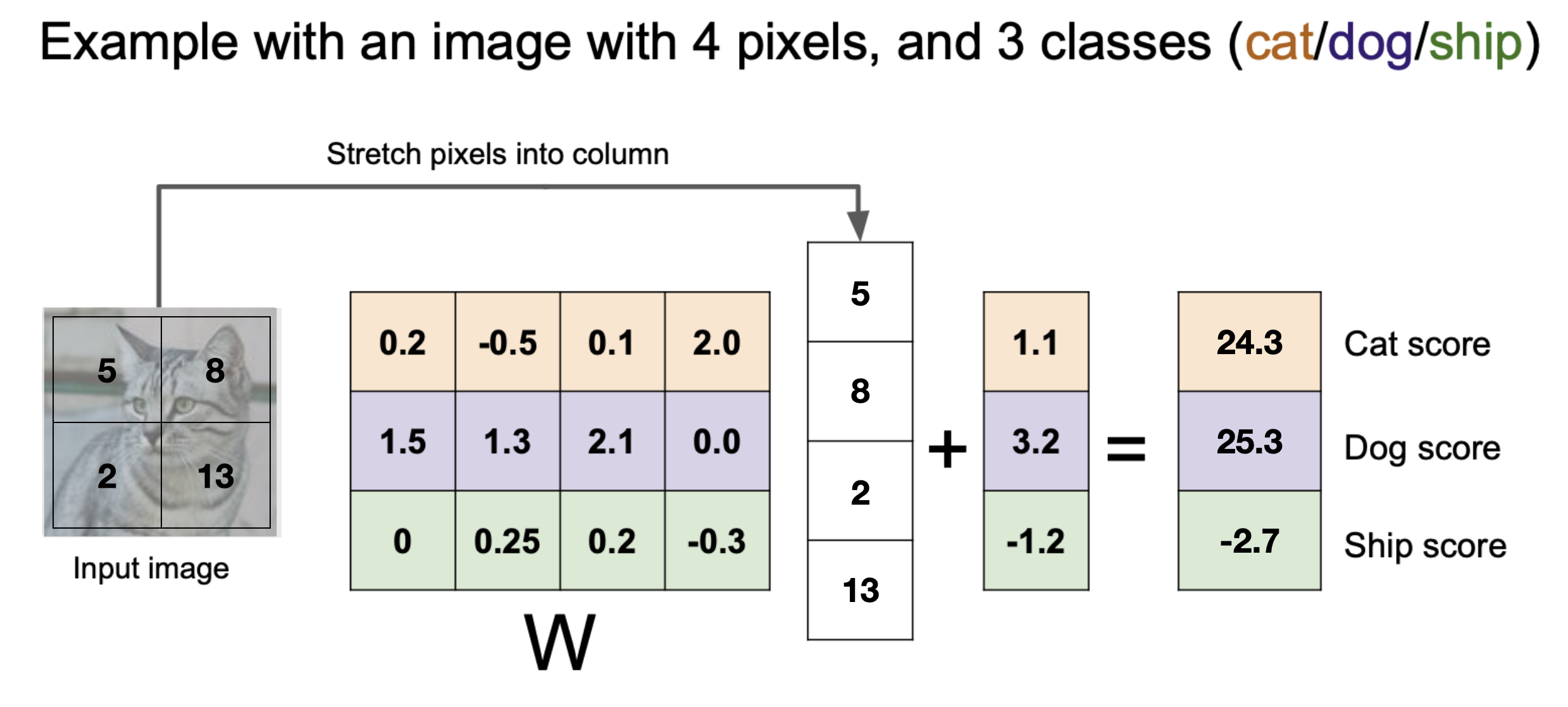
그 결과 스코어가 가장 높은 것은 Dog이므로, 이 이미지는 Dog로 분류된다. 잘못 분류된 셈이다. 우리의 분류기 파라미터는 아직 충분히 좋지 못한 셈이다. 우리의 분류기 성능을 올리기 위해서는, 현재 분류기의 성능 척도를 정의하고, 그 척도로부터 무언가를 배울 수 있어야 한다.
Let a given dataset:
Loss over the dataset is a average of loss over examples:
이런 방식으로 평균 로스를 계산하고, 이것이 높을 수록 성능이 낮다고 정의할 수 있다.
여기서 아직 정의되지 않은 것은 물론, 개별 로스를 정의하는 방법이다.
이는 경우에 따라 다르다. 로스를 어떻게 정의할지는 설계자의 손에 달려있다.
가장 먼저 소개할 방법은 흔히 사용되는 Softmax + Cross-entropy이다.
Softmax Loss
앞서 구한, Cat, Dog, Ship의 스코어를 그대로 사용하여 로스를 구할 수도 있지만,
소프트맥스를 통해 정규화하면, 표현상에 더 많은 이점이 있다.

이후 cs224n 강의 참고하여, 크로스엔트로피 설명.
및 SVM내용 추가
Interpreting a Linear Classifier: Visual Viewpoint
이 외에도 수많은 데이터를 통해 학습이 완료된 분류기, 즉 파라미터 W의 각 행은 해당 분류를 위한 무언가 기준이 되는 표본으로서의 이미지를 띠게될 것이다. 이를 템플릿templete이라고 하는데 이를 이미지화한 템플릿을 관찰하면 분류기의 내적에서 어떤일이 일어나는지 대략 짐작해볼 수 있다.

위 그림 하단에 보면 10개의 클래스가 갖는 각각의 템플릿들을 확인할 수 있다.
하지만 보이듯 각 템플릿들은 굉장히 이상하다. 예컨대 horse 클래스의 경우 말 비스무리하게 생겼지만, 머리가 양쪽에 모두 달려있는 것 같다. 왜냐하면 어떤 이미지의 경우 왼쪽에 머리가 있고 또 어떤 경우에는 오른쪽에 머리가 있기 때문이다. 이처럼 문제는 각 클래스에 대해 단 하나의 템플릿만을 학습하기 때문에 한 클래스 내에 존재하는 다양한 특징들을 평균화 시켜서 갖게 된다는 것이다.
추후 배울 Neural Network와 같이 더 복잡한 모델에서 이를 해결할 것이다.
Interpreting a Linear Classifier: Geometric Viewpoint
분류기 f가 무엇을 하는 지에 대한 또 다른 시각적 관점이 있다.
위 CIFAR10예시에서, 이미지 픽셀값 x는 3072차원 벡터이기 때문에 선형함수 f는 다음과 같다.
각 클래스에 대한 score가 선형결합 Wx + b임을 생각하자. 3072 차원 함수를 시각화할 수는 없지만, 모든 차원을 두 차원으로 압축하여 상상하면, 분류기가 하는 일을 시각화해볼 수 있다.
그러면, Linear Classifier가 각 클래스를 구분하는 선형경계를 학습하고 긋는 모습을 상상할 수 있다.
다음은 3072 차원으로 이루어진 각 이미지를 고차원 공간의 한점으로 표현한 모습이다.

여기서 보이듯, W의 각 행은 클래스 중 하나에 대한 분류기이다.
이러한 Linear Classification이 직면할 수 있는 아래와 같은 문제들이 있다는 것도 참고하자.

Training without Overfitting
그런데 파라미터 학습 시에 데이터를 무작정 학습할 시에는 오버피팅이 발생할 수 있다.
만약, 아래 그림의 Idea 1처럼 데이터 세트를 모두 train set으로 사용하고, 그 정확도로 성능을 평가한다면 학습 데이터가 아닌 데이터에 대해서는 좋은 성능을 보일 수 없게된다. 그냥 해당 데이터에 오버피팅된 파라미터값이 되어, 한 번도 본적없는 데이터에 대한 유의미한 예측값을 나타내지 못한다.
따라서 Idea 2처럼 일부 데이터는 학습에 사용하지 않고 test를 통한 성능 척도로만 사용하는 시도를 할 수 있다. 이 경우 train 데이터 자체를 나타내는 학습이 발생하지는 않겠지만, 여러 하이퍼파라미터 중 test 데이터에서만 높은 성능을 나타내는 하이퍼파라미터로 오버피팅이 발생하게 된다. 이것은 정확한 성능을 표현하지 못한다.
그렇기 때문에 validation set을 추가로 할당하여 이를 통해 검증하고, test는 완전히 간접적으로나마 터치되지 않은 데이터로 놔두어 검증할 수 있게 된다.

즉, 파라미터에 대한 오버피팅을 피하기 위해 하나. -validation
하이퍼파라미터에 대한 오버피팅을 피하기 위해 또 하나를 두는 셈이다. -test
(좀 더 쉬운 관점으로는 그냥 test 세트에 대한 오버피팅을 피하기 위해 validation 세트를 둔다고 봐도 좋다.)
하지만 이와 같은 validation 세트가 train 세트를 대표하지 못할 수도 있다. 데이터가 적은 경우 더욱 그렇다. 그런 경우, Cross-Vaildation 방법을 통해 일반화 성능을 향상시킬 수 있다.
Cross-Validation
훈련 세트를 n 분할하여 돌아가며 valid set으로 사용하여 평균을 낸다. 아래의 경우 5분할이므로 대략 훈련 데이터가 5배 많은 것처럼 학습할 수 있다.

하지만, 학습에 긴 시간이 걸리는 딥러닝에서 이 방법은 잘 사용되지는 않지만, 논문의 재현성 등을 위한 일반화 성능 향상을 위해서는 더 권장되는 방법이긴 하다.